Estadística : Manejo de la Informacion

1.- MANEJO DE LA INFORMACIÓN

La investigación cuya finalidad es: el análisis o experimentación de situaciones para el descubrimiento de nuevos hechos, la revisión o establecimiento de teorías y las aplicaciones prácticas de las mismas, se basa en los principios de Observación y Razonamiento y necesita en su carácter científico el análisis técnico de Datos para obtener de ellos información confiable y oportuna.
Este análisis de Datos requiere de la Estadística como una de sus principales herramientas, por lo que los investigadores de profesión y las personas que de una y otra forma la realizan requieren además de los conocimientos especializados en su campo de actividades, del manejo eficiente de los conceptos, técnicas y procedimientos estadísticos

1.1 MUESTREO

El muestreo es por lo tanto una herramienta de la investigación científica, cuya función básica es determinar que parte de una población debe examinarse, con la finalidad de hacer inferencias sobre dicha población. La muestra debe lograr una representación adecuada de la población, en la que se reproduzca de la mejor manera los rasgos esenciales de dicha población que son importantes para la investigación. Para que una muestra sea representativa, y por lo tanto útil, debe de reflejar las similitudes y diferencias encontradas en la población, es decir ejemplificar las características de ésta.
En estadística se conoce como muestreo a la técnica para la selección de una muestra a partir de una población.Al elegir una muestra aleatoria se espera conseguir que sus propiedades sean extrapola bles a la población. Este proceso permite ahorrar recursos, y a la vez obtener resultados parecidos a los que se alcanzarían si se realizase un estudio de toda la población.Cabe mencionar que para que el muestreo sea válido y se pueda realizar un estudio adecuado (que consienta no solo hacer estimaciones de la población sino estimar también los márgenes de error correspondientes a dichas estimaciones), debe cumplir ciertos requisitos. Nunca podremos estar enteramente seguros de que el resultado sea una muestra representativa, pero sí podemos actuar de manera que esta condición se alcance con una probabilidad alta.En el muestreo, si el tamaño de la muestra es más pequeño que el tamaño de la población, se puede extraer dos o más muestras de la misma población. Al conjunto de muestras que se pueden obtener de la población se denomina espacio muestral. La variable que asocia a cada muestra su probabilidad de extracción, sigue la llamada distribución maestral.

EJEMPLOS:

1.-Suponga que estamos investigando sobre el porcentaje de alumnos que trabajan de una población de 20 alumnos de una Universidad

Base de datos de la población:

Nombre Alumno ¿Trabaja?
Juan SI
María NO
Alicia NO
Fernanda NO
Pedro NO
Julio SI
Marcos NO
Rosa NO
Alberto SI
Fabián NO
Jorge SI
Ana NO
José NO
Laura NO
Carlos NO
Enrique NO
Miguel NO
Carmen SI
Victoria SI
Marcelo SI

2.-Se tiene a la siguiente población de personas clasificadas como consumidores de drogas:
Nombre Droga
Felipe Alcohol
Wilma Marihuana
José Pasta Base
Viviana Cocaína
Pablo Alcohol
Rodrigo Marihuana
Carlos Extasis
Catherine Alcohol
Claudia Marihuana
Valentina Neoprén
Enrique Marihuana

3.-

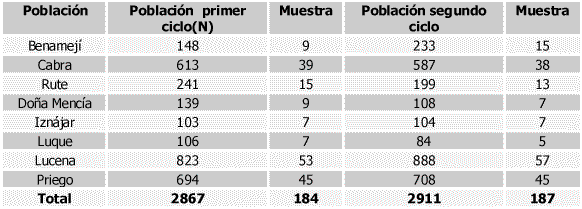
1.2 FRECUENCIA

En Estadística, frecuencia es el número de veces que el valor de una variable se repite. Se distinguen dos tipos principales de frecuencia: relativa y absoluta.

Frecuencia de clase

es el numero de mediciones que se pueden agrupar en una clase en una tabla o distribución de frecuencia

Clase

es un intervalo o subconjunto de una escala que se utiliza para comparar mediciones o características que pertenecen a un elemento muestral y determinar cuales por su magnitud o cualidad le pertenece

Frecuencia relativa

Es el resultado de la división entre el valor de la frecuencia absoluta (ni) y el tamaño de la muestra (N). Se suele representar de esta forma: fi . Puede aparecer de forma decimal, como fracción o como un porcentaje.

Frecuencia relativa acumulada

es la suma de la frecuencia relativa de todas las clases anteriores a la clase ¡ mas la de esta

Formula:

Frecuencia Relativa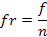

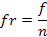
Ejemplos:

1.-

2.-

3.-

1.3 DISTRIBUCIÓN DE FRECUENCIA

Una distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.Frecuencia absolutaLa frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.Se representa por f_i.La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N.Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma mayúscula) que se lee suma o sumatoria.

Ejemplos:

1.-

2.-

3.-

1.4 REPRESENTACIÓN GRÁFICA E INTERPRETACIÓN

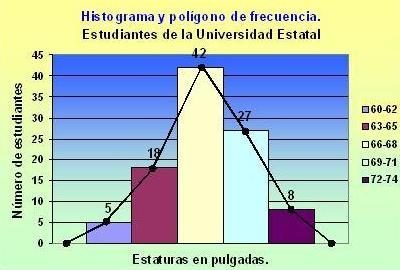
Histograma de Frecuencias

Los histogramas son diagramas de barras verticales en los que se construyen barras rectangulares en los límites de cada clase. La variable aleatoria o fenómeno de interés se despliega a lo largo del eje horizontal; el eje vertical representa el número, proporción o porcentaje de observaciones por intervalo de clase, dependiendo de si el histograma particular, es un histograma de frecuencia, un histograma de frecuencia relativa o histograma de porcentaje.
Representaciones tabulares, frecuencias Una vez obtenida una muestra de cualquier población y observados los valores que toma la variable en los individuos de la muestra, estos valores se suelen ordenar. Si la variable es cuantitativa la ordenación será de menor a mayor .

Frecuencia absoluta n_i.- es el número de veces que aparece en la muestra dicho valor de la variable.
Frecuencias acumuladas f_i.- la suma de cada frecuencia con la frecuencia de la clase contigua superior.
Frecuencias relativas N_i.- Dividiendo cada frecuencia entre el número total de observaciones y multiplicándolas por l00 para tenerlas en forma de porcentaje.
Frecuencias relativas acumuladas F_i.- La suma de cada frecuencia relativa con la frecuencia relativa de la clase contigua superior. También se pueden obtener dividiendo cada frecuencia acumulada entre el total de frecuencias por l00.
La distribución de frecuencia es la representación estructurada, en forma de tabla, de toda la información que se ha recogido sobre la variable que se estudia en la muestra o población originales.