2.1 MEDIA ARITMÉTICA
Es un promedio que en datos no agrupados se obtiene de la suma de los valores dividida entre el total de los datos

Para datos agrupados se obtiene de la suma por la frecuencia de cada clase por su marca de clase entre el numero de datos

Ejemplos:
1.- Datos agrupados

2.- Datos no agrupados

3.-

2.2 MEDIANA
Es un promedio que se ubica justo a la mitad de los datos, dividiéndola en dos partes iguales

Ejemplos:
1.- Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla:
| Calificaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Número de alumnos | 2 | 2 | 4 | 5 | 8 | 9 | 3 | 4 | 2 |
Primero se hallan las frecuencias absolutas acumuladas  . Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene
. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene 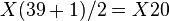 .
.
 . Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene
. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene 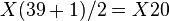 .
.- Ni-1< n/2 < Ni = N19 < 19.5 < N20
Por tanto la mediana será el valor de la variable que ocupe el vigésimo lugar.En este ejemplo, 21 (frecuencia absoluta acumulada para Xi = 5) > 19.5 con lo que Me = 5 puntos, la mitad de la clase ha obtenido un 5 o menos, y la otra mitad un 5 o más.
| xi | fi | Ni |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 2 | 4 |
| 3 | 4 | 8 |
| 4 | 5 | 13 |
| 5 | 8 | 21 > 19.5 |
| 6 | 9 | 30 |
| 7 | 3 | 33 |
| 8 | 4 | 37 |
| 9 | 2 | 39 |
2.-Entre 1.50 y 1.60 hay 2 estudiantes.
Entre 1.60 y 1.70 hay 5 estudiantes.
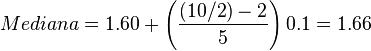 3.- Hallar la mediana de la distribución estadística que viene dada por la siguiente tabla:
3.- Hallar la mediana de la distribución estadística que viene dada por la siguiente tabla:
| fi | |
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |
| fi | Fi | |
| [10, 15) | 3 | 3 |
| [15, 20) | 5 | 8 |
| [20, 25) | 7 | 15 |
| [25, 30) | 4 | 19 |
| [30, 35) | 2 | 21 |
| 21 |


2.3 MODA
Es un promedio que consiste en el dato o datos que se repiten con mayor frecuencia. puede no existir.


Ejemplos:
1.-Calcular la moda de la distribución estadística:
| fi | |
|---|---|
| [0, 5) | 3 |
| [5, 10) | 5 |
| [10, 15) | 7 |
| [15, 20) | 8 |
| [20, 25) | 2 |
| [25, ∞) | 6 |

2.-Calcular la moda de una distribución estadística que viene dada por la siguiente tabla:

| fi | |
|---|---|
| [60, 63) | 5 |
| [63, 66) | 18 |
| [66, 69) | 42 |
| [69, 72) | 27 |
| [72, 75) | 8 |
| 100 |

3.-Calcular la moda de una distribución estadística viene dada por la siguiente tabla:

| fi | |
|---|---|
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |

2.4 MEDIA GEOMÉTRICA
La media geométrica (MG) de un conjunto de números estrictamente positivos (X1, X2,…,XN) es la raíz N-ésima del producto de los N elementos.
 Todos los elementos del conjunto tienen que ser mayores que cero. Si algún elemento fuese cero (Xi=0), entonces la MG sería 0 aunque todos los demás valores estuviesen alejados del cero.
Todos los elementos del conjunto tienen que ser mayores que cero. Si algún elemento fuese cero (Xi=0), entonces la MG sería 0 aunque todos los demás valores estuviesen alejados del cero.
Ejemplos:
1.-En una empresa quieren saber la proporción media de mujeres en los diferentes departamentos. Para ello, se recoge el porcentaje de mujeres en los cinco principales departamentos.




3.-

2.5 MEDIA ARMÓNICA
La media armónica (H) de un conjunto de elementos no nulos (X1, X2,…,XN) es el recíproco de la suma de los recíprocos (donde 1/Xi es el recíproco de Xi)) multiplicado por el número de elementos del conjunto (N).

La media armónica es la recíproca de la media aritmética. Los elementos del conjunto deben ser necesariamente no nulos. Esta media es poco sensible a los valores grandes, pero muy sensible a los valores próximos a cero, ya que los recíprocos 1/Xi son muy altos.

Ejemplos:
1.- Un tren realiza un trayecto de 400km. La vía tiene en mal estado que no permitían correr. Los primeros 100 km los recorre a 120km/h, los siguientes 100km la vía está en mal estado y va a 20km/h, los terceros a 100km/h y los 100 últimos a 130km/h. Para calcular el promedio de velocidades, calculamos la media armónica.

La media armónica es de H=52,61km/h.



excelente blog con información detallada para comprender de una forma clara y precisa
ResponderBorrar