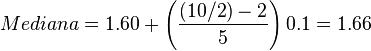3.1 RANGO
Es el intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con lel fin de obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto.El rango (R) o recorrido estadístico es la diferencia entre el valor máximo y el mínimo de un conjunto de datos.

Ejemplos:
1.- Supongamos que deseamos calcular el rango de las edades del once inicial de un equipo de fútbol.

El jugador más mayor (máximo del conjunto) tiene 31 años, mientras que el más joven (mínimo) 18. Por lo tanto el rango es:


El jugador más mayor (máximo del conjunto) tiene 31 años, mientras que el más joven (mínimo) 18. Por lo tanto el rango es:

2.-

3.-
3.2 DESVIACIÓN MEDIA
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por



Ejemplos:
1.-Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


| fi | |
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |
| xi | fi | |x − x | · fi | |
| [10, 15) | 12.5 | 3 | 27.857 |
| [15, 20) | 17.5 | 5 | 21.429 |
| [20, 25) | 22.5 | 7 | 5 |
| [25, 30) | 27.5 | 4 | 22.857 |
| [30, 35) | 32.5 | 2 | 21.429 |
| 21 | 98.571 |
Media

Desviación media

| xi | fi | xi · fi | |x - x| | |x - x| · fi | |
| [10, 15) | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
| [15, 20) | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
| [20, 25) | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
| [25, 30) | 27.5 | 4 | 110 | 5.714 | 22.856 |
| [30, 35) | 32.5 | 2 | 65 | 10.174 | 21.428 |
| 21 | 457.5 | 98.57 |


3.3 DESVIACIÓN TÍPICA
La desviación típica es la medida de dispersión (S) asociada a la media. Mide el promedio de las desviaciones de los datos de una muestra (X1,X2,…,XN) de la media (x) en las mismas unidades de los datos. Dicho de otra forma, es un indicador de cómo tienden a estar agrupados los datos respecto a la media.

El cuadrado de la desviación típica es la varianza.
Cuando se trata de la desviación típica de una población, el denominador es N. Si se trata de una muestra, será N-1.
Desviación típica para datos agrupados


Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.




Ejemplos:
1.-Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


2.- Calcular la desviación típica de la distribución de la tabla:9, 3, 8, 8, 9, 8, 9, 18


| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


3.-El número de veces que va al cine en un mes cada componente de un grupo de once amigos es:
2, 2, 2, 3, 1, 2, 1, 3, 1, 1, 4
1
0.95

3.4 VARIANZA
La varianza se representa por
 .
.

Varianza para datos agrupados


Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.


1.- Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


2.- Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


3.- Un médico de un instituto quiere realizar un estudio para ver si los alumnos de un centro tienen sobrepeso. Le interesaría calcular la varianza para ver como difieren los pesos respecto a la media. Para ello, se selecciona una muestra de doce alumnos de 14 o 15 años.

Se calcula la media de los pesos de los alumnos, y se obtiene que x = 53,5kg.
Una vez se sabe la media, se halla la diferencia de cada elemento respecto a esta, para calcular la dispersión de los datos.

Una vez se ha calculado el cuadrado de la diferencia de cada elemento con la media, ya se puede determinar lavarianza (S2):

El valor alto de la varianza confirma una de sus características: que es sensible a los valores que se separan bastante de la media.
A continación se puede observar un gráfico de las diferencias del peso de cada alumno respecto a la media:







 . Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene
. Así, aplicando la fórmula asociada a la mediana para n impar, se obtiene 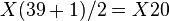 .
.